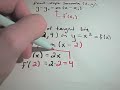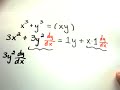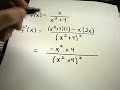This course offers a comprehensive introduction to the foundations of calculus, specifically focusing on:
This playlist is structured to follow a typical calculus class sequence, though individual exploration of specific topics is encouraged. Videos are designed to provide intuitive explanations and detailed examples to aid learning.